激活函数

激活函数(Ativation function)肯定不是线性的函数，激活函数通过把特征通过映射(到非线性函数)的方式表达出来，可以解决线性函数表达能力弱的问题。

常用激活函数

sigmoid

采用S形函数，取值范围[0,1]

sigmoid 是使用范围最广的一类激活函数，具有指数函数形状，它在物理意义上最为接近生物神经元。此外，(0, 1) 的输出还可以被表示作概率，或用于输入的归一化，代表性的如 Sigmoid 交叉熵损失函数。

sigmoid 也有其自身的缺陷，最明显的就是饱和性。从上图可以看到，其两侧导数逐渐趋近于 0 。具有这种性质的称为软饱和激活函数。具体的，饱和又可分为左饱和与右饱和。与软饱和对应的是硬饱和。一旦输入落入饱和区，f′(x) 就会变得接近于 0，导致了向底层传递的梯度也变得非常小。此时，网络参数很难得到有效训练。这种现象被称为梯度消失或梯度弥散。

此外，sigmoid 函数的输出均大于 0，使得输出不是 0 均值，这称为偏移现象，这会导致后一层的神经元将得到上一层输出的非 0 均值的信号作为输入。

tanh

双切正切函数，取值范围[-1,1]

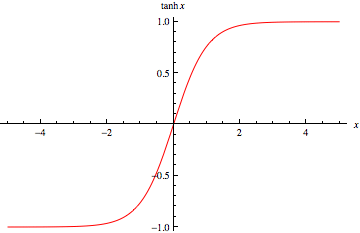
tanh 也是一种非常常见的激活函数。与 sigmoid 相比，它的输出均值是 0，使得其收敛速度要比 sigmoid 快，减少迭代次数。然而，从途中可以看出，tanh 一样具有软饱和性，从而造成梯度消失。

ReLU

简单而粗暴，大于0的留下，否则一律为0。

当 x<0 时，ReLU 硬饱和，而当 x>0 时，则不存在饱和问题。所以，ReLU 能够在 x>0 时保持梯度不衰减，从而缓解梯度消失问题。这让我们能够直接以监督的方式训练深度神经网络，而无需依赖无监督的逐层预训练。

然而，随着训练的推进，部分输入会落入硬饱和区，导致对应权重无法更新。这种现象被称为 “神经元死亡()”。与 sigmoid 类似，ReLU 的输出均值也大于 0，偏移现象和神经元死亡会共同影响网络的收敛性。

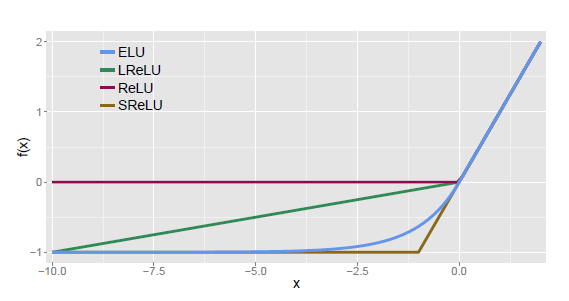
P-ReLU, Leaky-ReLU, ELU

Leaky-ReLU:

P-ReLU:

ELU:

融合了 sigmoid 和 ReLU，左侧具有软饱和性，右侧无饱和性。右侧线性部分使得 ELU 能够缓解梯度消失，而左侧软饱能够让 ELU 对输入变化或噪声更鲁棒。ELU 的输出均值接近于零，所以收敛速度更快。在 ImageNet 上，不加 Batch Normalization 30 层以上的 ReLU 网络会无法收敛，PReLU 网络在 MSRA 的 Fan-in （caffe ）初始化下会发散，而 ELU 网络在 Fan-in/Fan-out 下都能收敛

Maxout

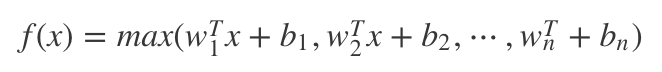
显然，Maxout是一个分段线性函数，而由于任意的凸函数都可由分段线性函数来拟合，所以，Maxout可以拟合任意的凸函数。

论文地址：https://arxiv.org/pdf/1302.4389

损失函数

常用损失函数

0-1损失

使用函数的正负号来进行模式判断，函数值本身的大小并不是很重要，0-1 损失函数比较的是预测值与真实值的符号是否相同，0-1 损失的具体形式如下：

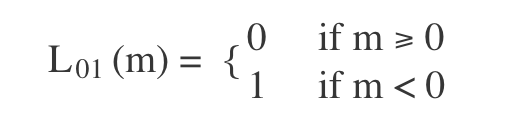
绝对值损失

平方损失

交叉熵损失

Original link：https://izhangzhihao.github.io//2017/11/25/Ativation-functions-and-loss-functions/